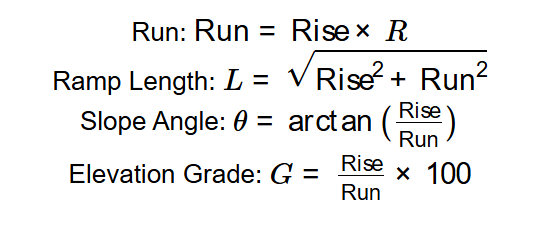Ramp Calculator

Rise (Vertical Height):

Slope Ratio:

Custom Rise-to-Run Ratio (e.g., 1:10):

Slope Angle:

Degrees (°)

Elevation Grade:

Percent (%)

Run (Horizontal Length):

Ramp Length:

Meters (m)

Ramp Slope calculator

Introduction

The Ramp Slope Calculator is an essential tool designed to compute the slope angle, elevation grade, run (horizontal length), and ramp length for a ramp based on its vertical rise and a selected or custom rise-to-run ratio. This calculator is invaluable for ensuring ramps are safe, accessible, and compliant with standards such as the Americans with Disabilities Act (ADA) or specific residential requirements.

Why is the “Ramp Slope Calculator” Important?

Accurate ramp slope calculations are critical for:

Accessibility: Ensuring ramps are usable by individuals with mobility challenges, such as wheelchair users, per ADA guidelines (e.g., 1:12 to 1:20 slopes).
Safety: Preventing overly steep ramps to reduce the risk of accidents, particularly for unassisted or assisted users.
Regulatory Compliance: Meeting building codes and accessibility standards for public spaces, commercial buildings, or residential settings.
Customization: Allowing flexibility to design ramps for specific scenarios, such as loading unoccupied wheelchairs or accommodating unique spatial constraints.

How the “Ramp Slope Calculator” Works

The calculator processes user inputs—rise (vertical height) and slope ratio—to compute four key outputs: slope angle, elevation grade, run, and ramp length. It converts the rise to meters, applies the rise-to-run ratio to determine the run, and uses geometric and trigonometric formulas to calculate the ramp length and slope characteristics. Results are formatted with four decimal places or scientific notation for very small values.

Formulas Used in the “Ramp Slope Calculator”

The calculator relies on the following equations, based on a rise-to-run ratio (e.g., 1:R):

Run: \( \text{Run} = \text{Rise} \times R \)
Ramp Length: \( L = \sqrt{\text{Rise}^2 + \text{Run}^2} \)
Slope Angle: \( \theta = \arctan\left(\frac{\text{Rise}}{\text{Run}}\right) \)
Elevation Grade: \( G = \frac{\text{Rise}}{\text{Run}} \times 100 \)

4.1. Where:

\( \text{Rise} \): Vertical height to overcome (in cm, m, in, ft, or yd).
\( R \): Run multiplier derived from the slope ratio (e.g., 12 for 1:12).
\( \text{Run} \): Horizontal length (in meters or feet).
\( L \): Ramp length, the hypotenuse (in meters or feet).
\( \theta \): Slope angle (in degrees).
\( G \): Elevation grade (in percent).

Step-by-Step Breakdown of the Formulas

The calculation process involves:

Input Rise and Unit: Enter the vertical height and select a unit (cm, m, in, ft, or yd).

Select Slope Ratio: Choose a predefined ratio (e.g., 1:12) or enter a custom ratio (e.g., 1:10).

Unit Conversion: Convert rise to meters for consistent calculations.

Calculate Run: Multiply rise by the run multiplier from the ratio.

Calculate Ramp Length: Use the Pythagorean theorem to find the hypotenuse.

Calculate Slope Angle: Apply the arctangent function to find the angle in degrees.

Calculate Elevation Grade: Compute the percentage of rise over run.

Output Conversion: Convert run and ramp length to the selected output unit (meters or feet).

Format Results: Display results with four decimal places or in scientific notation if the value is less than 0.001.

Example Calculation

6.1. Input Values

Rise: 0.5 meters
Slope Ratio: 1:12 (ADA maximum slope)
Output Unit: Meters

6.2. Calculation Steps

Run: \( \text{Run} = 0.5 \times 12 = 6 \, \text{m} \)
Ramp Length: \( L = \sqrt{0.5^2 + 6^2} = \sqrt{0.25 + 36} \approx 6.0208 \, \text{m} \)
Slope Angle: \( \theta = \arctan\left(\frac{0.5}{6}\right) \approx 4.7636^\circ \)
Elevation Grade: \( G = \frac{0.5}{6} \times 100 \approx 8.3333\% \)
Results: Slope Angle = 4.7636°, Elevation Grade = 8.3333%, Run = 6.0000 m, Ramp Length = 6.0208 m

Conclusion

The Ramp Slope Calculator simplifies the design of accessible and safe ramps by providing precise calculations for slope angle, elevation grade, run, and ramp length. It supports a variety of use cases, from ADA-compliant public ramps to custom residential designs, ensuring compliance and usability.

How to Use the “Ramp Slope Calculator”

8.1. Understanding the Input Fields

Rise: Enter the vertical height the ramp needs to overcome (e.g., 0.5 m or 24 in). Select a unit from cm, m, in, ft, or yd.
Slope Ratio: Choose a predefined ratio (e.g., 1:12 for ADA maximum) or select “custom” to enter a specific rise-to-run ratio (e.g., 1:10).
Custom Ratio: If “custom” is selected, input the ratio as “rise:run” (e.g., 1:10).
Output Unit: Select meters or feet for the run and ramp length results.

8.2. How to Interpret the Results

Slope Angle (°): The incline angle of the ramp, in degrees.
Elevation Grade (%): The steepness as a percentage (rise/run × 100).
Run: The horizontal length required, in the selected unit.
Ramp Length: The total length of the ramp (hypotenuse), in the selected unit.

Practical Applications & Expert Insights

9.1. Where the “Ramp Slope Calculator” is Used

Architecture and Construction: Designing ramps for public buildings, schools, and hospitals to meet ADA standards.
Residential Modifications: Creating accessible home entrances for wheelchair users or elderly individuals.
Event Planning: Setting up temporary ramps for festivals or outdoor venues.
Industrial Settings: Designing ramps for loading/unloading equipment or unoccupied wheelchairs.

9.2. Real-Life Scenarios

Public Accessibility: A city planner uses the calculator to design a 1:12 ramp for a new library, ensuring wheelchair access.
Home Renovation: A homeowner calculates a 2:12 slope for an assisted-use ramp to accommodate a family member’s mobility needs.
Construction Site: A contractor uses a custom 3:12 ratio to build a temporary ramp for loading wheelchairs onto a vehicle.

9.3. Expert Recommendations

ADA Compliance: For unassisted wheelchair users, aim for slopes between 1:16 and 1:20 for comfort and safety.
Landings: For ramps longer than 30 feet (9.14 m), include landings (minimum 60 in or 1.525 m) to meet ADA requirements.
Material Selection: Use non-slip surfaces and consider weather resistance for outdoor ramps.
Testing: Verify calculations with a physical mock-up to ensure usability before final construction.

Frequently Asked Questions (FAQs)

10.1. What is the Ramp Slope Calculator?

It’s a tool that calculates the slope angle, elevation grade, run, and ramp length based on the rise and a selected or custom rise-to-run ratio, aiding in the design of accessible ramps.

10.2. How is the slope of a ramp determined?

The slope is determined by the rise-to-run ratio (e.g., 1:12 means 1 unit of rise per 12 units of run). The calculator uses this to compute the angle, grade, run, and length.

10.3. Can the ramp slope be too steep?

Yes, slopes steeper than 1:12 are not recommended for unassisted wheelchair users per ADA standards, as they increase effort and risk. Steeper slopes (e.g., 3:12) are suitable for specific cases like unoccupied chairs.

10.4. Is there a maximum length for ramps?

ADA guidelines recommend landings every 30 feet (9.14 m) for unassisted users. The calculator focuses on straight segments; total length depends on landings and design.

10.5. What are the practical applications of ramp slope calculations?

They are used in designing accessible ramps for buildings, homes, events, and industrial settings, ensuring safety, compliance, and usability for mobility-impaired individuals.

10.6. Where can I find more information on ramp design?

Refer to the ADA Accessibility Guidelines (www.ada.gov), local building codes, or consult with accessibility experts and architects for detailed ramp design standards.